我們現在可以引入量子程式碼。我們的目標是了解如何保護透過雜訊通道傳輸的一組量子位元免受其遇到的任何錯誤的影響。該過程與經典程式碼類似，我們將採用 𝑘 量子位元並將其編碼為狀態 𝑛 量子位。然而，我們的任務將變得複雜，因為量子位元上的操作不僅僅是位元翻轉，而是有可能與環境產生任何形式的交互，例如相位翻轉或更一般的旋轉。幸運的是，我們會發現這種無限型別錯誤的可能性不會成為太大的障礙，我們可以建構出好的程式碼。

Setup

Alice 與Bob有一個有噪音的量子傳輸通道。總的來說，她打算傳遞𝑘-量子位元態給Bob。在傳輸過程中，量子態可能會出現錯誤 𝐸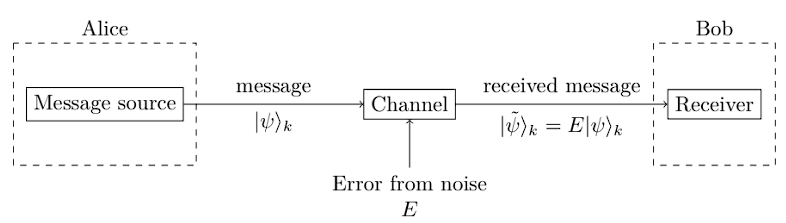

首先我們假設通道中有噪音，有機率為 𝑝 可以透過施加量子位翻轉運算子 𝑋 到它的每個量子位元。稍後我們將討論具有不同錯誤的通道。

假設一下 𝑘 = 1 。Alice 想傳送給 Bob單量子位元態 |𝜓⟩=𝛼|0⟩+𝛽|1⟩。如果她按原樣發送狀態，則有可能 ( 1 − 𝑝 ) Bob 收到狀態 | 𝜓⟩ 和機率 𝑝 Bob 收到狀態|⟩= 𝑋| 𝜓⟩ = 𝛽| 0⟩+𝛼|1⟩

Bob 不知道是否發生了錯誤。所以他不清楚 Alice 想要傳送什麼狀態。為了增加成功通信的機會，Alice和Bob應該使用量子糾錯碼。在抽象層面上，過程如下所示。

Encoding

在重複碼的量子版本中，Alice 取出未編碼的量子位，並以重複的方式將其編碼為三個量子位元的狀態。透過先註意基礎狀態的轉換可以最好地看出這一點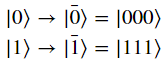

由此，我們可以確定量子位元態|𝜓⟩被編碼為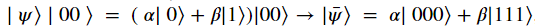

我們將原始量子位元稱為未編碼邏輯量子位元，將三個量子位元稱為資料量子位，以及它們的組合狀態 |⟩
編碼的邏輯量子位元。
編碼轉換可以使用以下量子電路來完成，該電路採用未編碼的邏輯量子位元和兩個狀態輔助 |𝜓⟩|00⟩
，到狀態中的編碼邏輯量子位 |⟩

import stac
enc_circ = stac.Circuit.simple(3)
enc_circ.append('CX', 0, 1)
enc_circ.append('CX', 0, 2)
enc_circ.draw()

狀態錯誤

Alice 透過雜訊通道傳送三個資料量子位元。他們每個人都會有機率 𝑝 被翻轉。如果第二個量子位元被翻轉，那麼鮑伯就會收到狀態 𝑋2|⟩ = 𝛼| 010⟩+𝛽|101⟩ 。總共有八種可能的錯誤，其機率與經典情況類似。

Error	Probility
I

Decoding

解碼分為三個部分

1. 確定發生了哪個錯誤。
2. 更正損壞的代碼字。
3. 將修正後的碼字轉回訊息（這部分也稱為解碼）。

偵測錯誤

假設只有集合中的錯誤 E= { I,𝑋1,𝑋2,𝑋3}發生時，Bob 必須 (a) 識別發生了哪些錯誤，以及 (b) 然後糾正它。他的任務比經典情況更困難，因為他無法測量接收狀態，因為這會破壞疊加，而且他獲得關於𝛼 和 𝛽的資訊很少，而這就是Alice真正想傳遞給Bob的內容。

相反，Bob追求的正確策略是進行部分測量，僅確定其中一個量子位元是否與其他兩個不同。這是經典情況下多數投票演算法的替代，但非常相似。這種類型的測量不探測 𝛼 或者 𝛽 因此疊加得以維持。具體來說，鮑伯比較前兩個量子位元的值，並比較最後兩個量子位元的值。如果有差異，那麼他就會知道發生了哪個錯誤。以下電路完成此任務，其中需要兩個輔助量子位元。

用來偵測錯誤的輔助量子位元稱為校正子量子位元(syndrome qubits)。

synd_circ = stac.Circuit.simple(5)
synd_circ.append('CX', 0, 3)
synd_circ.append('CX', 1, 3)
synd_circ.append('TICK')
synd_circ.append('CX', 1, 4)
synd_circ.append('CX', 2, 4)
synd_circ.append('TICK')
synd_circ.append('M', 3)
synd_circ.append('M', 4)
synd_circ.draw()

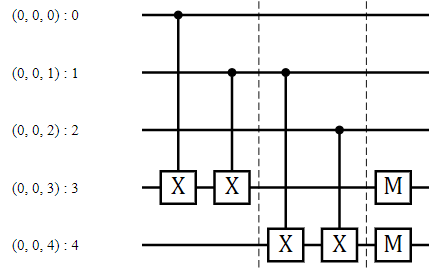
該電路由三個部分組成。在第一部分中，將第一和第二資料量子位元的值加到第一校正子量子位元。這是由 𝐶𝑋 閘實現
如果前兩個資料量子位元具有相同的值，則沒有一個 𝐶𝑋 閘將觸發或兩者都會觸發，因此校正子量子位元的值不會改變。從計算中可以看出，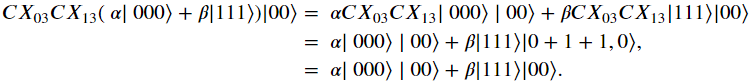

在這裡， 𝐶𝑋 閘不會觸發疊加中的第一項，但會觸發我們已明確說明的第二項。

如果前兩個資料量子位元不同，則只有其中一個 𝐶𝑋 門將會觸發。例如，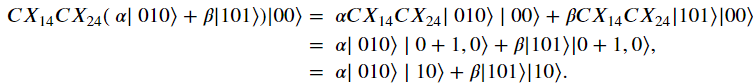

因此，syndrome qubits的值發生了翻轉。
除了第二和第三資料量子位元之外，電路的第二部分也會發生同樣的情況。隨後，測量兩個校正子量子位元。測量結果稱為綜合症，它們包含可以用來推斷發生了哪種錯誤的資訊。下表總結了這一點。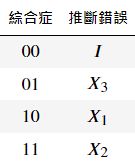

測試程式

使用下面的電路來測試這個推斷正確錯誤的過程

circ = stac.Circuit.simple(5)

# set message to |1> by uncommenting
# circ.append('X', 0)

# encode the state
circ.append('CX', 0, 1)
circ.append('CX', 0, 2)

# apply error to 0,1 or 2
circ.append('X', 0)

# do syndrome measurements
circ.append('CX', 0, 3)
circ.append('CX', 1, 3)
circ.append('TICK')
circ.append('CX', 1, 4)
circ.append('CX', 2, 4)
circ.append('TICK')
circ.append('M', 3)
circ.append('M', 4)

# sample the measurements
circ.draw()
# should be the syndrome
circ.sample()

更正錯誤

一旦Bob推斷出error，他就可以透過施加反相error來修復損壞的碼字。在這種情況下，錯誤運算子是自逆的，因此他只需再次使用它們來修復損壞的碼字，例如。如果他認為錯誤 𝑋1 發生了，他施加 𝑋1 到損壞的狀態來修復它。

Decoding

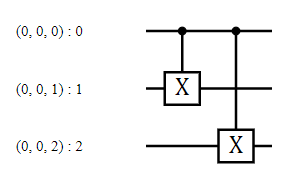
最後，Bob 可以撤銷編碼操作以恢復 Alice 想要傳送的單量子位元狀態。由於編碼操作是自逆的，Bob只需通過 |⟩ 透過它來恢復 | 𝜓⟩

dec_circ = stac.Circuit.simple(3)
dec_circ.append('CX', 0, 1)
dec_circ.append('CX', 0, 2)
dec_circ.draw()

參考資料:https://github.com/abdullahkhalids/qecft